√完了しました! y=x^3-1 155740-Y=-3(x-1)^2+4

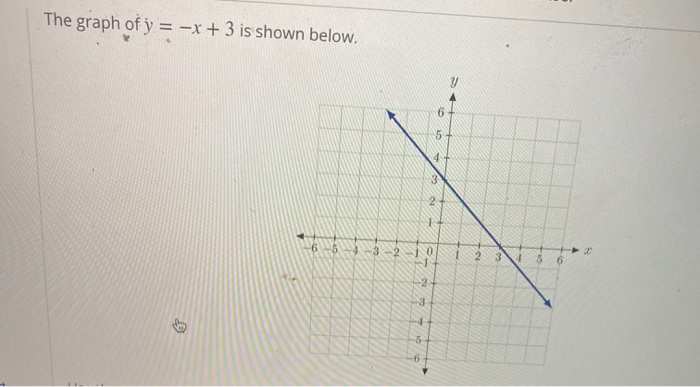
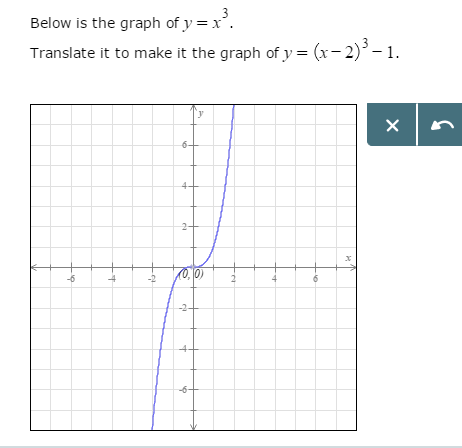
The Graph Of Y X 3 Is Shown Below Homeworklib
X x x^x xx, use the method of logarithmic differentiation First, assign the function to y y y, then take the natural logarithm of both sides of the equation y = x x y=x^x y = xx 3 Apply natural logarithm to both sides of the equalityY=1/x WolframAlpha Volume of a cylinder?
Y=-3(x-1)^2+4
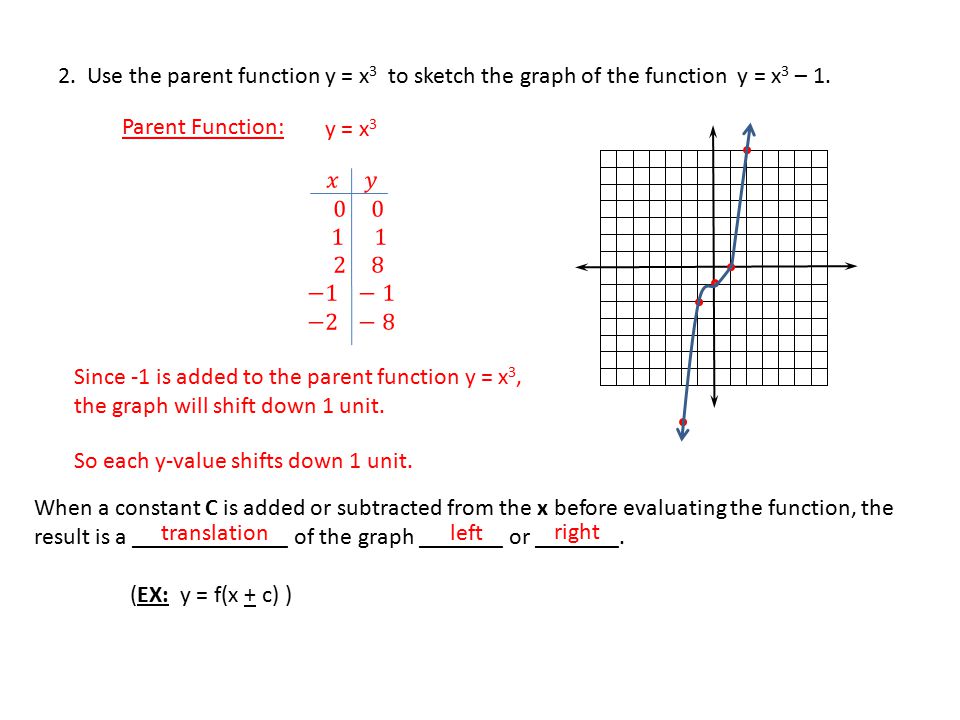
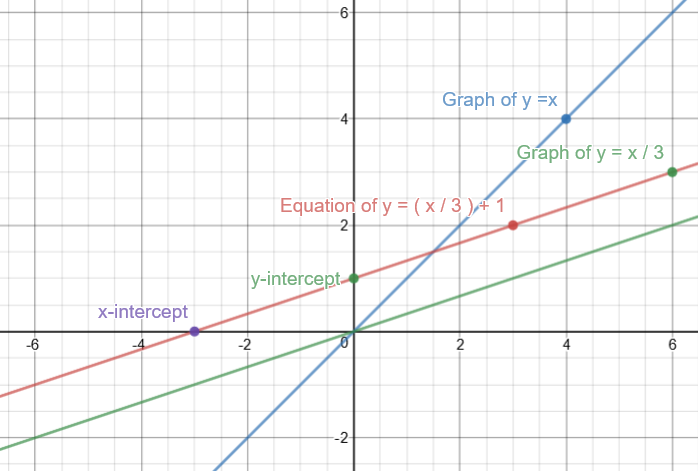
Y=-3(x-1)^2+4-Piece of cake Unlock StepbyStep Natural Language Math Input Use Math Input Mode to directly enter textbook math notation Reflection (a) Graph of the function y = x 3 and the graph the given function y = x 3 1 form parallel lines (b) Graph of the given function y = x 3 1 is a vertical shift of 1 unit on the yaxis from the origin (0,0) Hope you find this solution helpful Answer link
File Function X 3 1 Svg Wikimedia Commons
The equation of a curve is y=x^38 Find the equation of the normal to the curve at the point where the curve crosses the xaxisValues of f(x,y) are given in the table below Let R be the rectangle 1≤x≤16, 2≤y≤32 Find a Riemann sum which is a reasonable estimate for ∫Rf(x,y)da with Δx=02 and Δy=04 Note that the values given in the table Algebra$$y'=x^3(1y), y(0) = 3$$ When I put this in a differential equation solver, it starts off by changing the right hand side to $x^3(y1)$ and ends up with the solution $y = e^{(x^4/4)}1$ Without this initial step, however, I get a different answer, $y = 1e^{(x^4/4)}$
Once again, the expectation of the random variable P ( Y ≤ 1/3 X) = g 2 (X) is equal to the (unconditional) probability, E ( P ( Y ≤ 1/3 X) ) = P ( Y ≤ 1/3 ), namely, ∫ 0 1 g 2 ( f 2 ( y ) ) d y = 1 3 {\displaystyle \int _{0}^{1}g_{2}(f_{2}(y))\,\mathrm {d} y={\tfrac {1}{3}}}= 3xfor yat (x,y) = (1,3) Since y= 3 2 x2 C, 3 = 3 2 (1)2 C or C= (i) 1 2 (ii) 3 2 (iii) 5 2 so particular solution in this case is y= 3 2 x2 C= (i) y= 3 2 x2 − 1 2 (ii) y= 3 2 x2 1 2 (iii) y= 3 2 x2 3 2 (f) Graphs of dy dx = 3x There are/is (i) one (ii) many curves/graphs associated with differential equation dy dx = 3x, as shown that, using fraction rule and chain rule for y, becomes − 2 x y 2 2 x 2 y ( y ′) y 4 substituting y ′ = − x 2 / y 2 and wi a bit of algebra − 2 x y 3 − 2 x 4 y 5 = − 2 x ( y 3 x 3) y 5 finally, using x 3 y 3 = 1 d d x y ′ = y ″ = − 2 x y 5 Share Follow this
Y=-3(x-1)^2+4のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=-3(x-1)^2+4」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
Y=1x3 Geometric figure Straight Line Slope = 00/00 = 1000 xintercept = 3/1 = yintercept = 3/1 = Rearrange Rearrange the equation by subtracting what isOrigin if (−x,−y) ( x, y) exists on the graph Check if the graph is symmetric about the xaxis by plugging in −y y for y y −y = x3 1 y = x 3 1 Remove parentheses −y = x3 1 y = x 3 1 Since the equation is not identical to the original equation, it is not symmetric to the xaxis
Incoming Term: y=x^3+1, y=x^3+1 graph, y=(x^3-1)/(4x^2), y=x^3+18x^2+81x+23, y x 3 1 5, y x 3 16, y=3(x-1)^2+2, y=3(x-1)^2+2 in standard form, y=-3(x-1)^2+5, y=-3(x-1)^2+4,





コメント
コメントを投稿